大家好，我想请教这样一个问题: 怎样构造一个区域，然后在该区域内取点？

这句话可能说的不是很清楚，请看一个二维平面的例子，

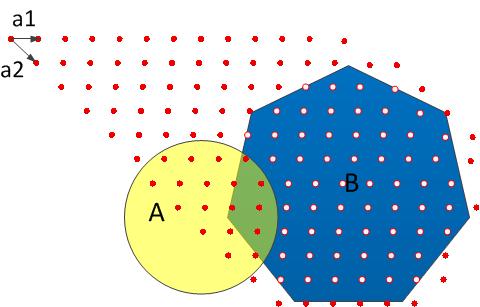
图中，B是一个凸多边形区域，A是一个圆形区域，我想在现在颜色为蓝色的区域生成格点。这个区域可以简单表示为 Region=RegionB-RegionA （RegionB与RegionA的补集的交集）。

然后我依据一组给定的基矢量（图中的a1和a2）在区域Region内生成所需的格点（如图中白色点所示），最终我得到的是格点的笛卡尔坐标值（或者在基a1、a2下的坐标）。

我的想法是这样的，应该有一些基本的构造区域的方法，例如：

1.      构造凸多边形的 A1=Region(类型=凸多边形，输入凸多边形顶点)，返回的A1就是一种区域类型的变量；

2.      构造圆形区域的 A2=Region(类型=圆，则输入圆心和半径)，

3.      构造半空间区域的 A3=Region(类型=半空间，则输入a，b)，返回A3为ax+b大于零的半空间区域

4.      …

这种区域类型支持交、并、补运算，进而能构造出新的复杂的区域。

最后，有这样的函数，能直接给出我想要的那些点：

XY=points(Region,a1,a2); #a1,a2为基矢量

应该说清楚了。我觉得这应该是一个很成熟的技术了吧，请问有没有大侠知道在python里怎么实现？其他语言，如MATLAB如果有的话，也请教教我。谢谢！

我写了一个例子，请打开下面的链接：

http://nbviewer.ipython.org/urls/dl.dropbox.com/s/kbsimhlb6gnadsp/shapely_gridpoints_in_polygon.ipynb

多谢啦！学习了！

竟然要FQ

RY大哥，我看了你的实现，感觉有几个小问题，想请教一下：

0. “将多边形转换到正交网格的坐标系”此句后的部分是多余的吧，

在此句前用

points_xzy = asMultiPoint(np.c_[X, Y])

region_xzy=np.array(region.intersection(points_xzy)).T

就能得到结果了

1. 程序中的“圆”并非真正的圆，而是用正N边形逼近的，因此有两个问题

1.1 为了得到就好的精度需要使用很大的N，这个感觉不太好

1.2 在判断点是否位于区域内时，应该是判断了一些线性不等式（形如ai*x+b>=0）是否都成立。换句话说，区域等价为一簇半空间的交集。

为了保证精度，对于圆就要使用很多个不等式。为什么不考虑用一个二次不等式来替换呢（a*x**2+b*y**2+c>=0）？

我看了shapely 的文档，里面并没有诸如circle这样的类型。是否说明shapely存在改善的空间，抑或这其中有什么是我没想到的？

你如果生成足够多的点，保证能覆盖多边形，那么就不需要“将多边形转换到正交网格的坐标系”。

进行坐标变换的目的是得出正交网格的范围。就是得出下面这句话中最佳的范围

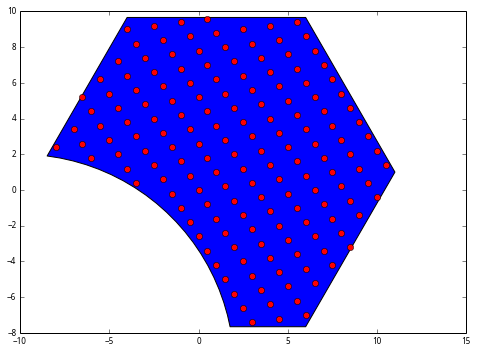
X2, Y2 = np.mgrid[-8:12, -12:12]

如果你的这个问题是为了解决一个实际的问题，多边形近似圆形是最简单的办法。如果要用圆形内部的不等式当然也可以，但是就不能事先对形状进行布尔操作了。

总结的步骤如下

1. 使用多边形近似圆形，并对区域进行布尔计算

2. 将区域变换到正交网格坐标系，求出正交网格中的范围

3. 根据范围使用a1和a2生成网格点

4. 找到网格点位于区域之内的点，如果要精确的话，就用圆形的公式。

原来是这样，不过我后来自己写了平行四边形投影变换限定了取值范围，

应该跟 affine_transform 实现了一样的功能。

感觉shapely最给力的功能就是区域的布尔操作了！